-
$$\mathbf{·}$$$$\mathbf{=}$$$$\mathbf{·}$$$$\mathbf{^{2}}$$
-
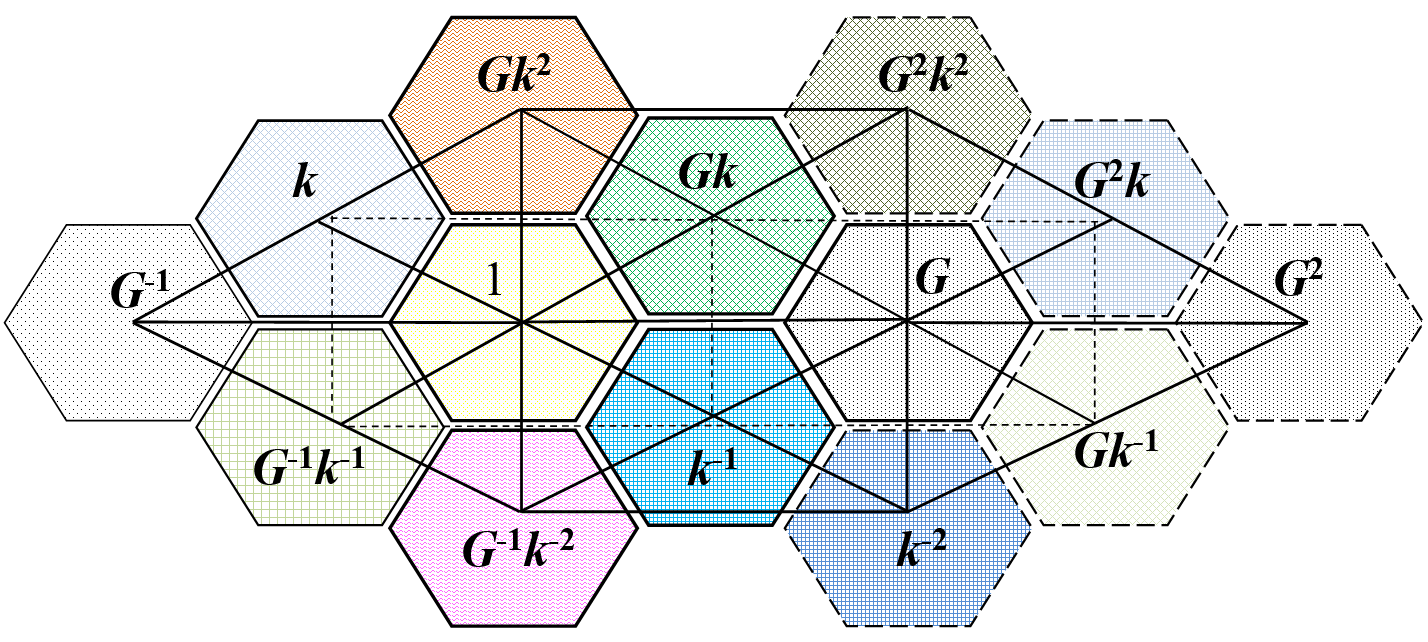
$$G$$$$\ ($$$$\mathbf{M^{-1}}$$$$)$$$$k^{-1}$$$$\ ($$$$\mathbf{M^{-1}}$$$$\mathbf{I}$$$$)$$$$G$$$$k$$$$\ ($$$$\mathbf{I^{-1}}$$$$)$$$$G^{-1}$$$$k^{-2}$$$$\ ($$$$\mathbf{M^{-1}}$$$$\mathbf{I^{2}}$$$$)$$$$G^{0}$$$$k^{0}$$$$\ ($$$$\mathbf{M^{0}}$$$$\mathbf{I^{0}}$$$$)$$$$G$$$$k^{2}$$$$\ ($$$$\mathbf{M}$$$$\mathbf{I^{-2}}$$$$)$$$$G^{-1}$$$$k^{-1}$$$$\ ($$$$\mathbf{I}$$$$)$$$$k$$$$\ ($$$$\mathbf{M}$$$$\mathbf{I^{-1}}$$$$)$$$$G^{-1}$$$$\ ($$$$\mathbf{M}$$$$)$$
-
+
-
Режим G
-
Режим k
-
Режим M
-
Режим I
-
n =
m =
-
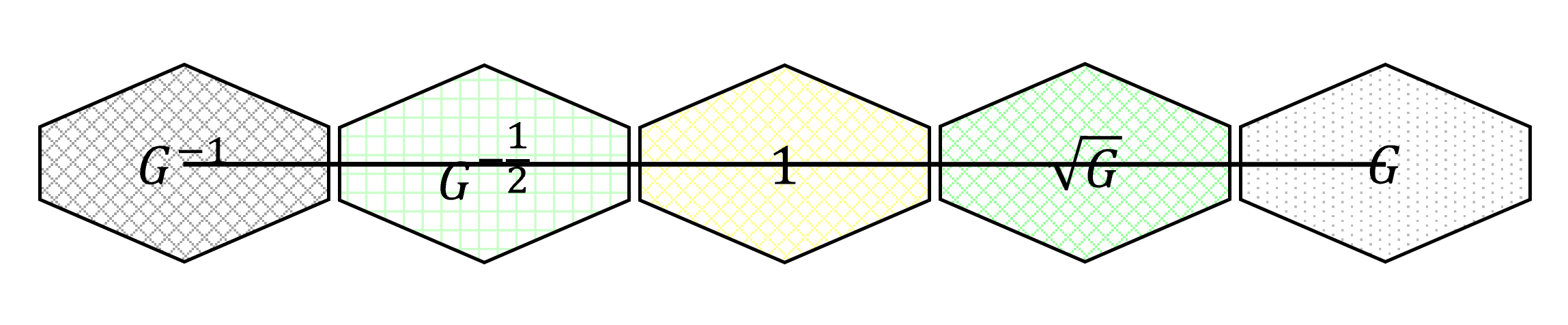
Режим G
-
Режим M
-
n =
-